电子—原子核双共振实验显示：施主电子的电荷和自旋都没有扩散。
19世纪数学家Dodson说过：“你使尽方法拼命地跑，以便维持在同一位置
(Now here，you see，it takes all the running you can do，to keep in the same place)”。
——引自安德森诺贝尔奖演讲词[1]
安德森局域化(Anderson localization)理论是凝聚态物理学中的一个重要且影响深远的理论，正式发表于1958年[2]。该理论预测的适用范围广泛，凡是电子波(函数)、电磁波、声波、地震波、弹性波等等，在一个充分强无序的系统中运动时，都有可能发生局域化现象，即波函数只分布在实空间的一个小区域中，而无法向四周扩散，遍布整个系统[3]。换句话说，波函数无法从样品的左边，经由一种类似布朗运动的扩散形式，一路传递至样品右边。(由于强无序造成的持续散射，波无法以直线前进，只能经由曲折蜿蜒的路径进行扩散运动。)若以固体中的局域化电子波函数为例，因为电子只在某微小区域中的出现几率(波函数振幅的平方|ψ|2)大于零，而在其他地方都为零(或说以指数形式快速减小趋近于零)，因此电子找不到一条贯通整个样品的路径，所以外加(小)偏压时，电流无法流通，样品不能导电，处于绝缘态。图1(a)显示的是电子平均自由程为l的延展波，图1(b)显示的是局域长度为ξ的局域波[4]。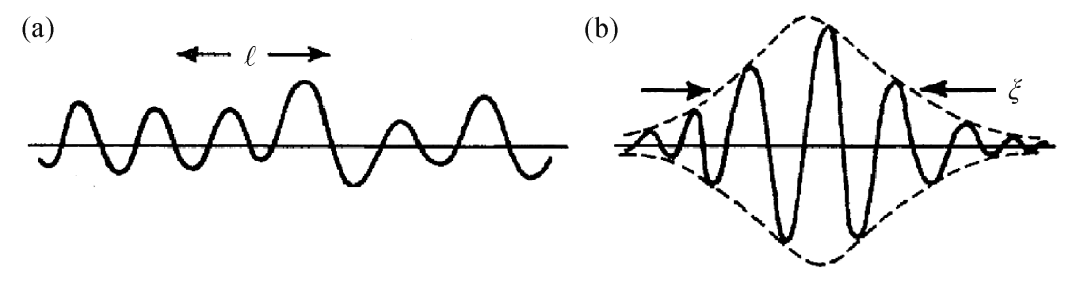
图1 (a)延展波示意图；(b)局域波示意图[4]
局域化的量子运动实体/单元(quantum-mechanical mobile entities)并不限于电子，在一个强无序系统中的自旋(波)也可能在适当条件下产生局域化现象。以n-型半导体磷掺杂硅晶体为例(图2)，五价施主磷原子的4个价电子用于与最近邻的4个硅原子形成共价键，剩下的一个价电子则与成键后晶格中的正一价(母)磷离子组成一个类氢原子，并有很大的轨道(约20 Å)。在液氦温度下，这个“施主电子(donor electron)”不会被电离，它除了电荷之外，也具有自旋(S=1/2)。当磷的掺杂浓度很低时(即样品在“金属—绝缘体转变”边界以下，处于绝缘态)，随机分布在硅晶体中的磷原子的平均距离较远，施主电子的自旋便会处于局域化状态，无法与周围的其他施主电子自旋产生自旋—自旋交换作用。这时，当该施主电子自旋方向若因故翻转(比如由向上转为向下)时，就无法带动邻近的施主电子自旋产生相反方向的翻转(比如由向下转为向上)，所以自旋状态的信息无法传递出去，没有发生自旋扩散，也就是自旋(波)局域化了。在安德森建立局域化理论的初始构思里，他心中所斟酌的，是想要建立一个广义的适用于各种量子实体/单元的局域化理论。他想要问一个与当时理论潮流逆向的问题：当晶格中的无序度够强时，量子实体/单元的扩散运动会不会逐渐趋缓，乃至完全停滞？安德森提问的具体对象是低浓度磷掺杂硅晶体的低温磁共振实验数据。当时，他在贝尔实验室的年轻同事George Feher发现在低掺杂浓度时，磷掺杂硅晶体中不但施主电子没有扩散，施主电子自旋也同样没有扩散，即不但没有发生杂质导电，而且施主电子自旋状态的信息也没有向外传递，表示两者都局域化了[5]。因此，安德森把他1958年的论文题目订定为广义的“Absence of diffusion in certain lattices”，他睿智地涵盖各种量子实体/单元(波)的扩散停滞，而不限定于电子的不能移动/导电。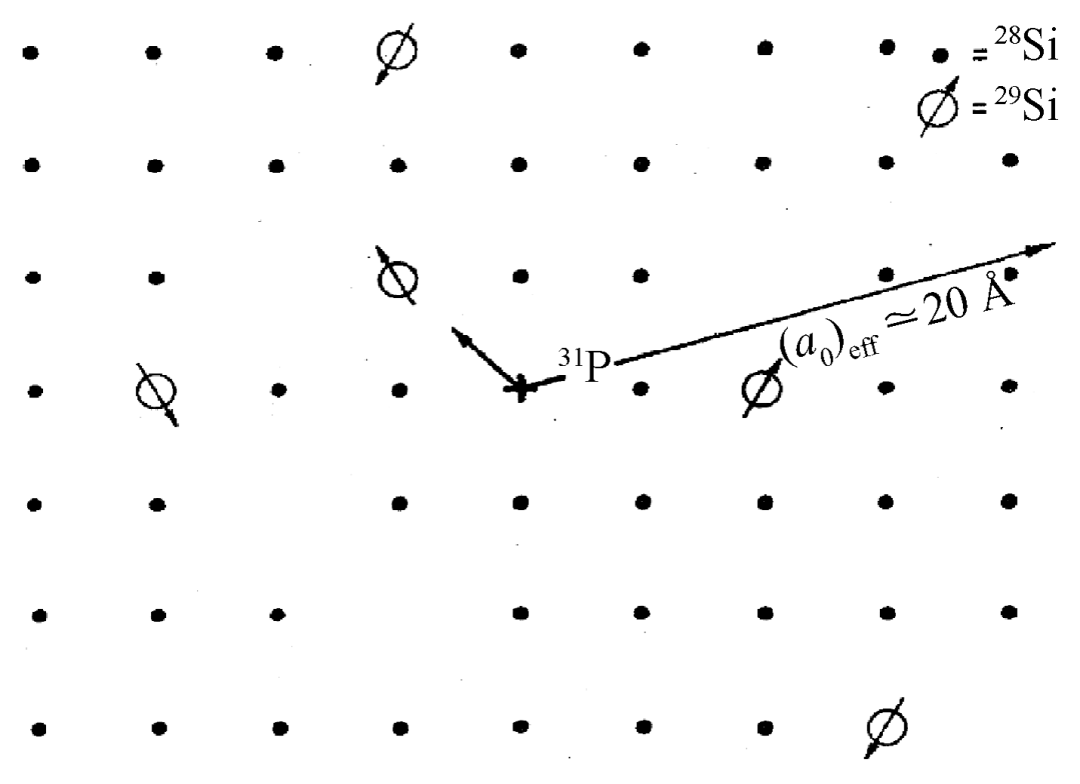
图2 磷掺杂硅晶体示意图[1]
再以磷掺杂硅晶体为例，从另一个角度说明何谓电子波函数的局域化。假设低温下和时间t=0时，施主电子与正一价(母)磷离子组成一个大轨道的类氢原子，处于基态。则问题可以表述为：经过一段长时间(t→∞)之后，在原点(母磷原子核)找到施主电子的几率(电子波函数振幅平方值|ψ(0)|2)为零吗？答案有两种可能性：(1)若|ψ(0)|2→0，表示电子跑掉了，扩散出去了，它是一个非局域波，或称延展波；(2)反之，若|ψ(0)|2>0，即表示它跑不掉，电子波函数(被多重散射的量子干涉结果)局域化了。与局域波空间分布性质相反的波称为延展波，如图1所示。在固体物理理论发展史上，1950年代的一个重要研究课题是如何建构金属晶体的量子力学电性传输理论[6]。由于真实的金属样品中都含有杂质或界面，导电电子在传输过程中会连续被散射，因此那时理论的重心都放在计算电子波函数遭遇散射之后如何产生电阻。因为晶体具有周期性的位势，其中导电电子波函数是延展性的(在整个晶体中都可以找到|ψ(r)|2大于零)，因此这些理论的出发点都直截了当地假设电子虽然受到了杂质的(频繁)散射，波函数必定仍是保持延展态的形式。事实上，直到安德森提出局域化理论并(经过了10多年)被物理学家广泛接受之前，电子“应该”能够贯穿整个系统形成延展态的概念与信念，深植人心。因为量子力学中有个扑朔迷离但确立无疑的隧穿效应，因此当时的物理学家一致认为即使掺杂浓度低，施主位置互相远离(平均距离远)，施主电子必定依然能够(在零温度和零偏压的情况下)藉由隧穿行为“跳到”周边的施主电子轨道，如此依序曲折前行(从晶格中的一点跳到邻近的一点)，终将导致杂质带的形成，使施主电子都具有延展态的波函数。再者，即使有些实验迹象和理论计算隐约显示施主电子并没有向四周扩散，大家也想当然地相信那一定是由于(莫特转变理论的)电子—电子相互作用阻挡了隧穿，绝不可能是强无序度导致了电子波的局域化。安德森局域化理论的出发点与其他量子电导理论的出发点背道而行，在仔细思考Feher的精细定量低温磁共振实验数据[5]之后，他非常敏锐地意识到一个问题，在一个无序系统中，如果无序程度足够强，施主电子自旋还能不能与周围的施主电子自旋进行交换耦合，进而造成自旋波的扩散呢？当时，根据实验数据，安德森的思考重心在于自旋的交换传递，远甚于关心电荷的扩散。在做出几项大胆的假设以及复杂的理论计算之后，安德森得出施主电子并没有跑离原点——它们跑不掉！——的结论，与Feher的实验结果吻合，这便是(至少对安德森本人而言)波的局域化的确立。安德森理论的两个主要假设是：(1)系统的无序足够强(超过某个临界值)；(2)忽略电子—电子相互作用。所以，安德森局域化理论是一个单电子理论。反之，莫特绝缘体则是由原子排列整齐有序的完美晶体中的强电子—电子库仑作用造成的，两个理论的假设前提迥异而涵盖范围和预测结果互补，都是探讨金属—绝缘体转变问题的重要指引和依据。1954年Feher博士毕业后加入贝尔实验室，他首先凭借着精湛技术和多年经验，立志自己率先开发建置一套极高分辨率磁共振(称为电子—原子核双共振，ENDOR)仪器，接着对磷掺杂硅进行了一系列精细繁复的低温测量。当时，晶体管主要都使用锗制造，因此贝尔实验室很支持对掺杂硅的深入研究，以便日后取代锗以制造性能更优越的晶体管之用。Feher测量施主电子自旋和母磷原子核自旋(S=1/2)，及和邻近29Si原子核自旋(S=1/2)交换作用产生的超精细结构，分析施主电子的运动状况，测得施主电子在这些原子核处的几率(|ψ(r)|2)[5]。(硅晶体中含有约4.7%的29Si同位素。)从这些实验结果，他发现施主电子并未(经由隧穿)扩散离开母磷原子，这一出人意表的结论是启发安德森另辟蹊径，创建局域化理论的关键实验数据！从这里我们学得一个启示：虽然Feher的磁共振实验数据发表于安德森文章的第二年，但并非秘密，当时有许多著名理论物理学家络绎于途来访或驻留贝尔实验室，他们大都知道实验结果，但是最终只有安德森洞烛机先，探骊得珠，这充分反映了他的非凡物理创见与学术功力。此外，安德森在建构局域化理论的过程中，并非仅凭一己之力独自耕耘，事实上他获得了好几位当时贝尔实验室理论学家的精辟、及时又无私的助力。安德森的这一项划时代成就，显示美国凝聚态物理学派的建立与长期睥睨全球，其中很多位我们耳熟能详的理论和实验大家，都是当时贝尔实验室的主人(研究员)或座上宾(访问学者)[1，7]。安德森的颠覆性局域化理论发表后10年之间，大约只被引用了30次，而且大多是来自莫特(Nevill Francis Mott)的引用。在众人还无法理解或仍不相信局域化理论的计算结果时，英国物理学家莫特非常重视波函数局域化的结论，他恍惚相信这是无序电子系统的重要微观概念，也应是描述低温导电行为的基石。那些年间，由于莫特全力发展金属—绝缘体转变、迁移率边和最小金属电导率等概念，又大力提倡低掺杂半导体中的变程跃迁理论，以及强调该导电过程的广义性，竟使得后学常误认为安德森局域化理论的出发点是为了解释无序系统的电学性质而来——低温时，电阻随温度下降而呈指数形式快速上升。可以说，局域化理论是一个绝对零度的理论，当温度大于零时，局域态之间可以藉由变程跃迁过程传递电子，造成导电[8]。莫特比安德森年长18岁，但他对安德森惺惺相惜，提拔有加。现今文献中金属—绝缘体相转变既有缺陷或杂质造成的无序引起的安德森转变，同时也有电子—电子库仑作用引起的莫特转变。关于变程跃迁导电的物理推导、曲折发展故事与争论，请见参考文献[9]。(在一个能带中，能带中间的态通常为延展态，而能带两端的态为局域态，分隔局域态和延展态的能量称为迁移率边)。通常，在我们谈到无序度时，总会直接想到固体中原子排列的不整齐、位错、空穴，或是晶体中掺杂了杂质。然而在安德森的理论中，他从晶格模型出发，假设每一个晶格点上的电子能量(Ej)是个任意值，随机分布在某个能量范围之内，例如：-W/2 ≤Ej≤W/2。对低浓度磷掺杂硅晶体而言，Ej相当于杂质能级能量，有高有低(此时电子波函数呈局域态，样品为绝缘性)。当杂质浓度逐渐增高并超过某一临界值时，离散的杂质能级将瞬间演化形成一条“杂质带”(此时电子波函数呈延展态，样品为金属性)。若考虑自旋问题，则Ej可视为施主电子自旋与母磷原子核自旋及与周遭29Si原子核自旋的超精细作用能量，因为29Si原子在硅晶格中有随机分布的位置，故Ej值也有个随机分布函数[2]。局域化理论发表之后，安德森的心思也随之转移了焦点，一方面是因为Feher离开了贝尔实验室，安德森不再经常到实验室串门子，另一方面则是前一年Bardeen—Cooper—Schrieffer (BCS)理论刚发表，超导体的研究正当道。另外，六年(1964)之后日本物理学家Jun Kondo也提出了近藤效应理论，造成另一股风潮。所以此后有20年的时间，安德森不曾再继续深入或延伸探索波的局域化问题[1]。1977年，安德森、莫特及John Van Vleck因为“对磁性和无序系统中的电子结构的基础性理论研究”，共同获得了诺贝尔物理学奖。次年，安德森与戴维·索利斯(David Thouless，2016年诺贝尔物理奖得主)在法国一起参加暑期学校，相处数周，他从Thouless那里学到了以e2/h作为电导(conductance，G)之基本单位的概念(e为电子电荷，h为普朗克常数)，又初窥了使用标度理论探讨各种维度和不同尺度固体的电导(G)性质的奥秘(Box 1)。在次年(1979)，安德森因缘际会，热情重燃，回头检验局域化理论的研究，与E. Abrahams、D. C. Licciardello和T. V. Ramakrishnan三人，提出了著名的局域化标度理论(scaling theory of localization)[10]，预测了二维弱局域化效应，并彻底改写了莫特金属—绝缘体相变理论中存在一个最小金属电导率的概念。莫特转变理论考虑电子平均自由程不能短于费米波长，因此金属电导率σ=ne2τ/m有一个下限值σmin=σ(kFℓ≈1)，式中n=n(kF)为电子密度，τ为电子散射时间，m为电子有效质量，kF为费米波数。局域化标度理论则从一个全新视角出发，完全舍弃了以电导率σ作为中心物理量，而改以电导G=G(L)，或无单位电导g(L)=G(L)/(e2/h)，作为理论中的唯一的标度参数(L为样品尺度)。在安德森局域化理论中，波函数的空间分布范围称做局域长度(ξ)。因为波函数的振幅随离开原点的距离以指数形式衰减，因此在ξ范围之外电子出现的几率指数衰减趋近于零，即电子跑不出去，因此无法导电。实验上，如果样品的大小为Ld(L为边长，d为维度)，则安德森强局域化现象的最直接表现将是样品的低温电导随样品尺度增大而呈指数形式减小，即G(L)∝exp(-L/ξ)。在二维方块样品中，电导等于电导率(G=σ)，或写成方块电导等于方块电导率(G□=σ□)。一般而言，给定一个无序固体材料，电导率(电阻率的倒数)的大小与边长L无关，符合欧姆定律。
图3显示处于电中性点(CNP)的反点阵列石墨烯纳米结构(nano‐structured antidot graphene)方块样品在源极—漏极电压为20 mV和2 K下的电导值(G□)随样品边长的变化关系，图中数据包括边长各为2、4、6、8及10 μm的5个方形样品，和边长大于10 µm的3个方形样品[11]。红色实线显示边长小于10 μm时，ln[G□/G0]∝-L，即G□=G0exp(-L/ξ)，这里G0为一常数。黑色空心圆是图中那些反点阵列石墨烯样品在远离电中性点(门极电压高12 V)时，样品已离开强局域区域而进入弱局域区域，此时方块电导与样品尺度无关。若不计光波、声波等经典波，图3应是对电子波出现了强局域现象的最直接实验观测[12]。(相对于光波而言，光子之间没有相互作用，电子之间则有库仑作用，因此测量无序电子系统的强局域现象别具高度挑战性。)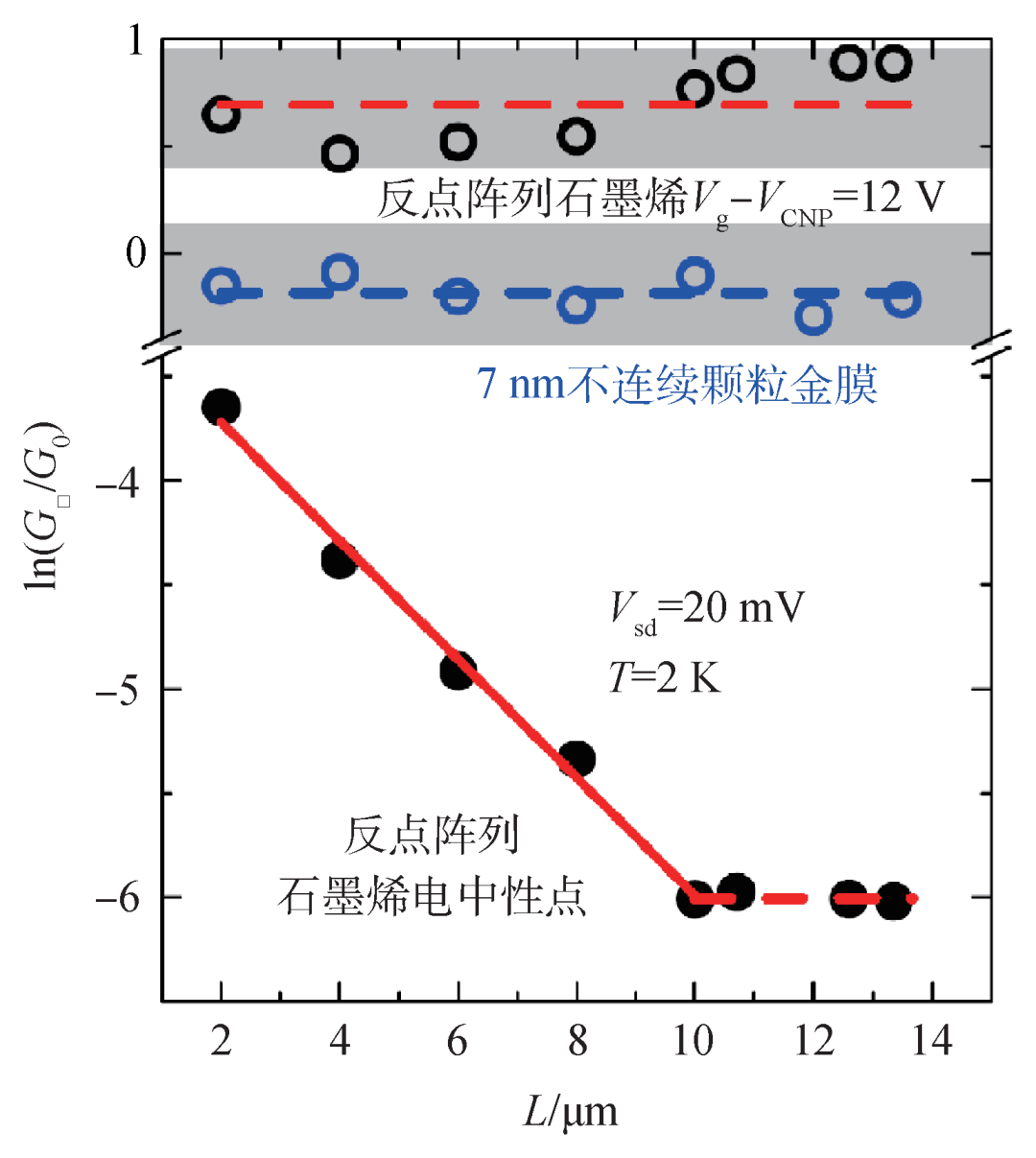
图3 纳米结构石墨烯的低温方块电导随样品边长呈指数形式减小[11]
要观测到如图3中的安德森强局域化行为，电子在样品内必须维持相位相干性，即相位相干长度Lφ大于局域长度，且符合Lφ>L>ξ>ℓ不等式关系。这是一个很严苛的条件，实验很难达成。如图3中的蓝色空心圆圈所示，7 nm厚的颗粒金膜的低温方块电导值与方形样品边长无关，因为在一般的无序金属中，电子平均自由程小于相位相干长度，又小于局域长度，即ℓ<Lφ<L<ξ。在安德森建构局域化理论时(1956—1958年)，Elihu Abrahams是位刚获得学位不久的年轻学者，他参与了很多讨论和计算。20年后，他在建立局域化标度理论的过程中，扮演了重要角色，是该篇(也是)划时代论文的领衔作者(1979年)。2013年年底，美国普林斯顿大学为安德森主办了一场盛大的学术会议，庆祝他的90岁生日，许多重量级学者都参与盛会并发表演说。有趣的是，除了回顾并前瞻强/弱局域化理论的过去与将来，Abrahams还特地指出贝尔实验室G. J. Dolan和Douglas D. Osheroff (1996年诺贝尔物理奖得主)的低温金属薄膜电导测量，是及时证实了局域化标度理论预测的第一个实验。Abrahams的演说论文正式发表于2016年[13]，两年之后，他就去世了。关于Dolan—Osheroff实验不曾印证二维弱局域化效应，但是不仅Abrahams，安德森和Osheroff两人也都终生以为该实验结果与理论预测完全吻合的阴错阳差的故事，请见参考文献[14]。莫特的金属—绝缘体相变理论预测二维和三维系统中都存在一个最小金属电导率(σmin)，划分了绝缘态(σ<σmin)和金属态(σ>σmin)，因此随着无序度逐渐增强(或减弱)，金属到绝缘体的相变(绝缘体到金属的相变)是一种不连续性的突然相变。在莫特获得诺贝尔物理学奖两年之后，局域化标度理论就否定了二维系统存在金属—绝缘体相变的旧理论——局域化标度理论预测(绝对零度时)二维系统都是绝缘体。(原始局域化标度理论并未考虑自旋—轨道耦合作用，若自旋—轨道耦合很强，会造成反局域化现象，称为弱反局域化(weak anti-localization)效应。)同时，局域化标度理论虽然预测了三维系统存在金属—绝缘体相变，但又预测该相变是连续性的，否定了莫特的有个σmin的旧理论。(一个边长够长的二维系统一定是绝缘体，即系统中的量子实体/单元在经过长时间的扩散运动之后，返回原点的几率趋近于1，请见参考文献[15]。三维系统的情况则完全相反，除非有很强无序度，否则返回原点的扩散几率趋近于零。)1977年12月，安德森在诺贝尔奖颁奖典礼的演讲中说，局域化理论发表之后几年，许多人，甚至包括作者本人都不相信强无序能导致波局域化，而能够看出局域化理论重要性的人更是少之又少。许多年后，局域化理论成为了显学，炙手可热，于是风水轮流转，它常常被许多论文攀附引用，记得安德森曾经在某个场合，既感慨又开玩笑，而且不无几分骄傲地说过一句话：“我的名字常常被用于描述我从来没有听过的现象 (My name has been used to describe many phenomena of which I have never heard)”。最后总结两点，一是长江后浪推前浪，江山代有才人出。科学有走偏的时刻，但有更多时候，科学(家们)总能依循正途、砥砺前行。二是有一个或许值得寄语年轻一代去开拓探索的问题是：在新颖材料中，如拓扑材料、量子材料、二维材料等，波的局域化将会如何发生，进而影响、展现与衍生新的物理现象？
致 谢感谢香港科技大学沈平教授、中央大学杨仲准教授、辅仁大学吴至原副教授、阳明交通大学叶胜玄助理教授、北京大学马中水教授、天津大学李志青教授，及德国马克思·普朗克固体化学物理研究所张海婧研究员在本文发表前的仔细阅读和提供修改意见。[1] Anderson P W. Review of Modern Physics，1978，50：191(安德森诺贝尔演讲论文)
[2] Anderson P W. Phys. Rev. Lett.，1958，109：1492
[3] Lagendijk Ad，van Tiggelen B，WiersmaD S. Physics Today，2009，62 (8)：24
[4] Lee P A，Ramakrishnan T V. Review ofModern Physics，1985，57：287
[5] Feher G. Physical Review，1959，114：1219
[6] Kohn W，Luttinger J M. Physical Review，1957，108：590
[7] Zangwill A. A Mind Over Matter-PhilipAnderson and the Physics of the VeryMany. Oxford University Press，2021
[8] 关于变程跃迁/杂质导电过程，请参考：Huang Y L，Chiu S P，Zhu Z X et al.Journal of Applied Physics，2010，107：063715；关于杂质带导电机制，请参考：Chiu S P，Lin Y H，Lin J J. Nanotechnology，2009，20：015203
[9] 林志忠 . 物理，2021，50 (8)：553；林志忠. 物理，2021，50 (9)：634
[10] Abrahams E，Anderson P W，Licciardello D C et al. Phys. Rev. Lett.，1979，42：673
[11] Zhang H，Lu J，Shi W et al. Phys. Rev.Lett.，2013，110：066805
[12] 张海婧，沈平. 物理，2013，42 (07)：456
[13] Abrahams E. Some Reminiscences onAnderson Localization. In：Chandra P，Coleman P，Kotliar G et al. edited.PWA90：A Lifetime of Emergence. Singapore：World Scientific Publishing，2016
[14] 林志忠. 物理，2022，51 (11)：800
[15] Sheng P. Introduction to Wave Scattering，Localization and Mesoscopic Phenomena，second edition. Berlin：Springer，2006. p.10
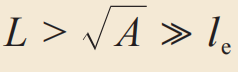(准一维)。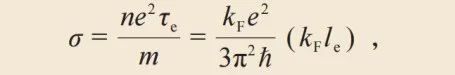
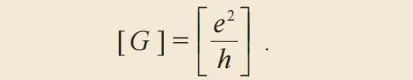
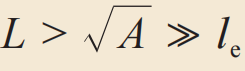。外加小偏压后，如电流能够顺畅流通整条细线，则(在液氦温度以上)系统为金属性，电阻对温度的变化遵循三维玻尔兹曼传输方程式的描述。
